Exploring Point Processes

Workshop 1: The Poisson Process

Author

Dr Zak Varty

Session Outline

  1. Recap
  2. The Poisson Process
  3. Formal Definitions
  4. Useful Properties & Areas for Further Exploration

Recap: What is a Point Process?

Defining a Point Process

A point process is a stochastic process where:

  • RVs \(\{X_1, \ldots, X_N\}\) represent localised events on some (typically continuous) mathematical space \(S\).

  • We are interested in value and number of events, but both of these are random.

  • Events \(X \in S\) vs. points / locations \(s \in S\).

Example: Temporal point process

Example: 1D point process

Example: 2D point process

The Homogeneous Poisson Process

  • Number of events is Poisson distributed, \(N \sim \text{Pois}(\lambda |S|)\).

  • Events located independently of one another, uniformly at random over \(S\).

In the 2D context, this is known as complete spatial randomness.

HPP as a central case

cells_path <- here::here("data/cells.csv")
pines_path <- here::here("data/black_pines.csv")
redwoods_path <- here::here("data/redwood_seedlings.csv")

cells <- readr::read_csv(cells_path, show_col_types = FALSE)
pines <- readr::read_csv(pines_path, show_col_types = FALSE)
redwoods <- readr::read_csv(redwoods_path, show_col_types = FALSE)
Figure 1: Locations of 42 cell centres in a unit square (Ripley 1977).
Figure 2: Locations of 65 Japanese black pine saplings in a square of side 5.7 m (Numata 1961).
Figure 3: Locations of 62 redwood seedlings in a square of side 23 m (Strauss 1975; Ripley 1977).

Trying to reference Figure 1.

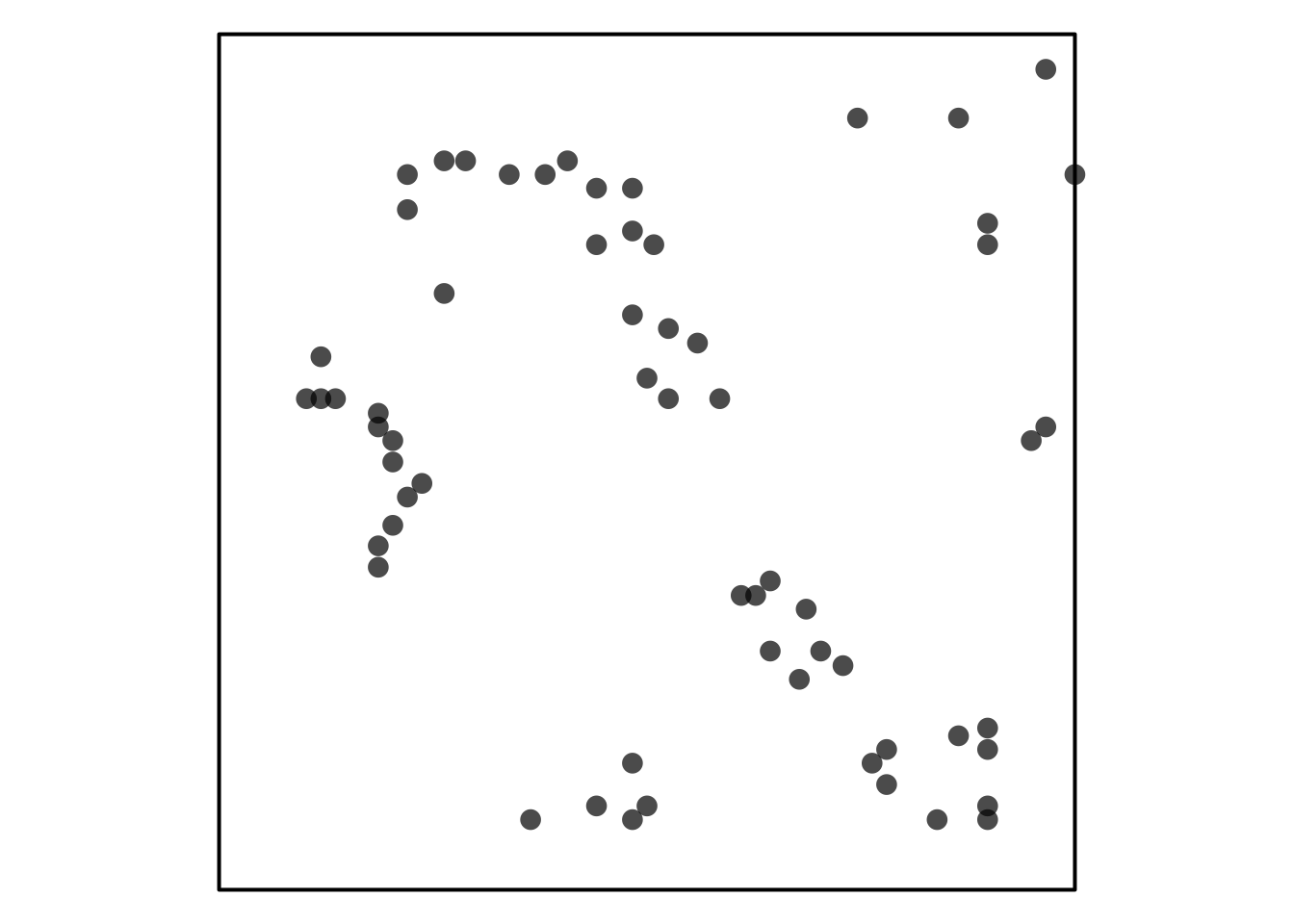
Visual Assessment of CSR

Some simulated point patterns - which is random, clustered or repulsive?

Figure 4
Figure 5
Figure 6
Suggested Poster Topic
  • How can you assess whether a particular point pattern satisfies CSR?

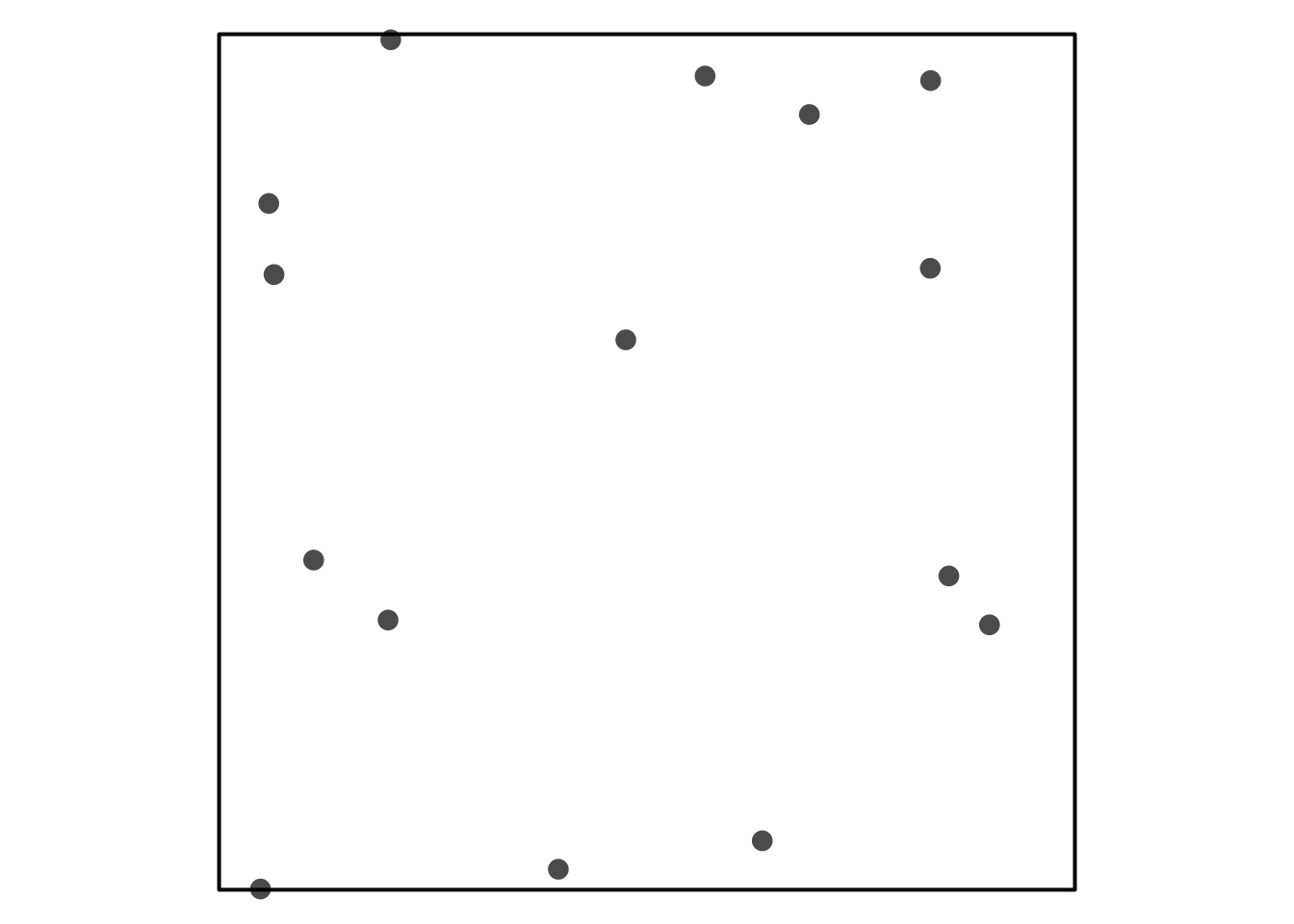
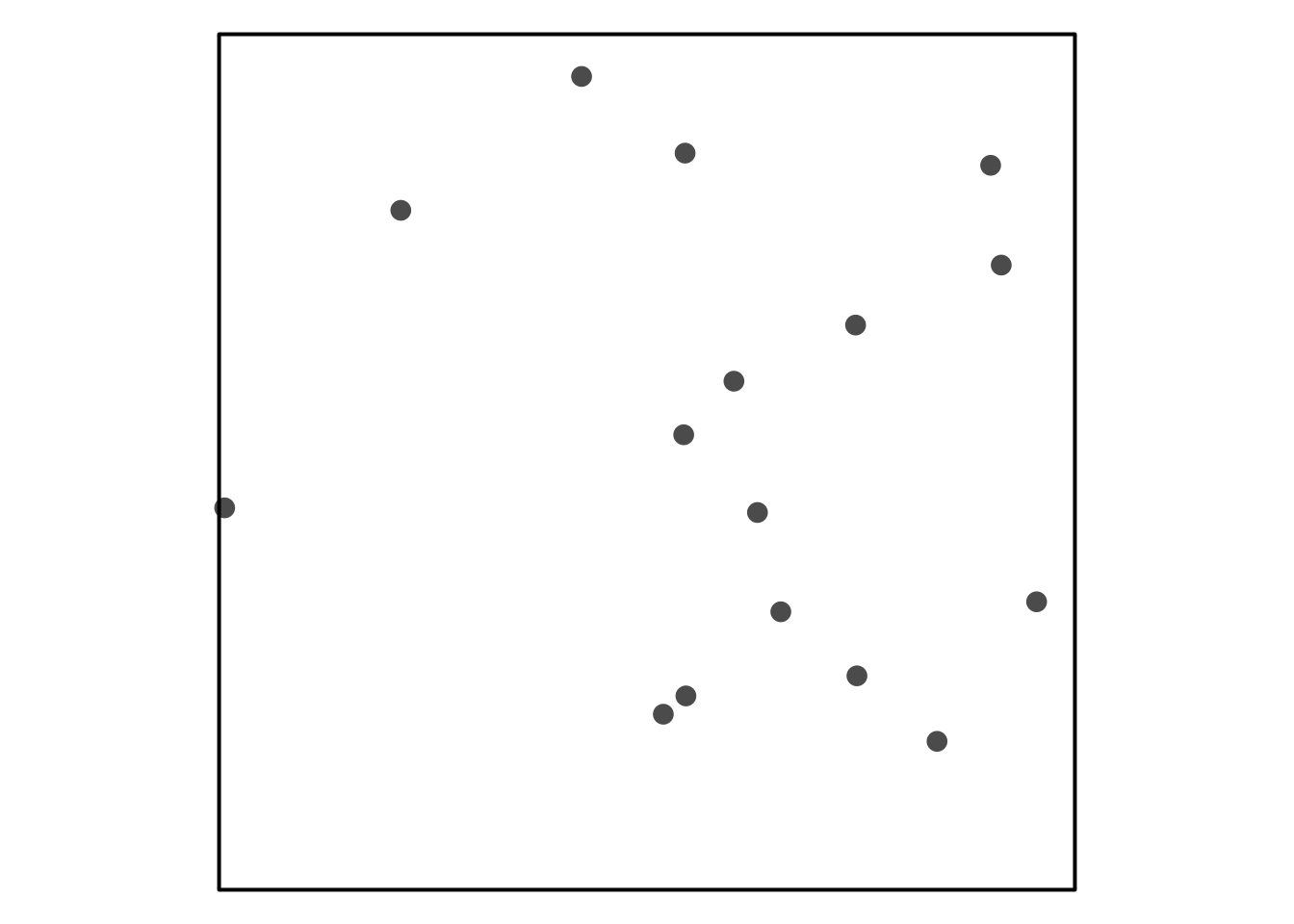
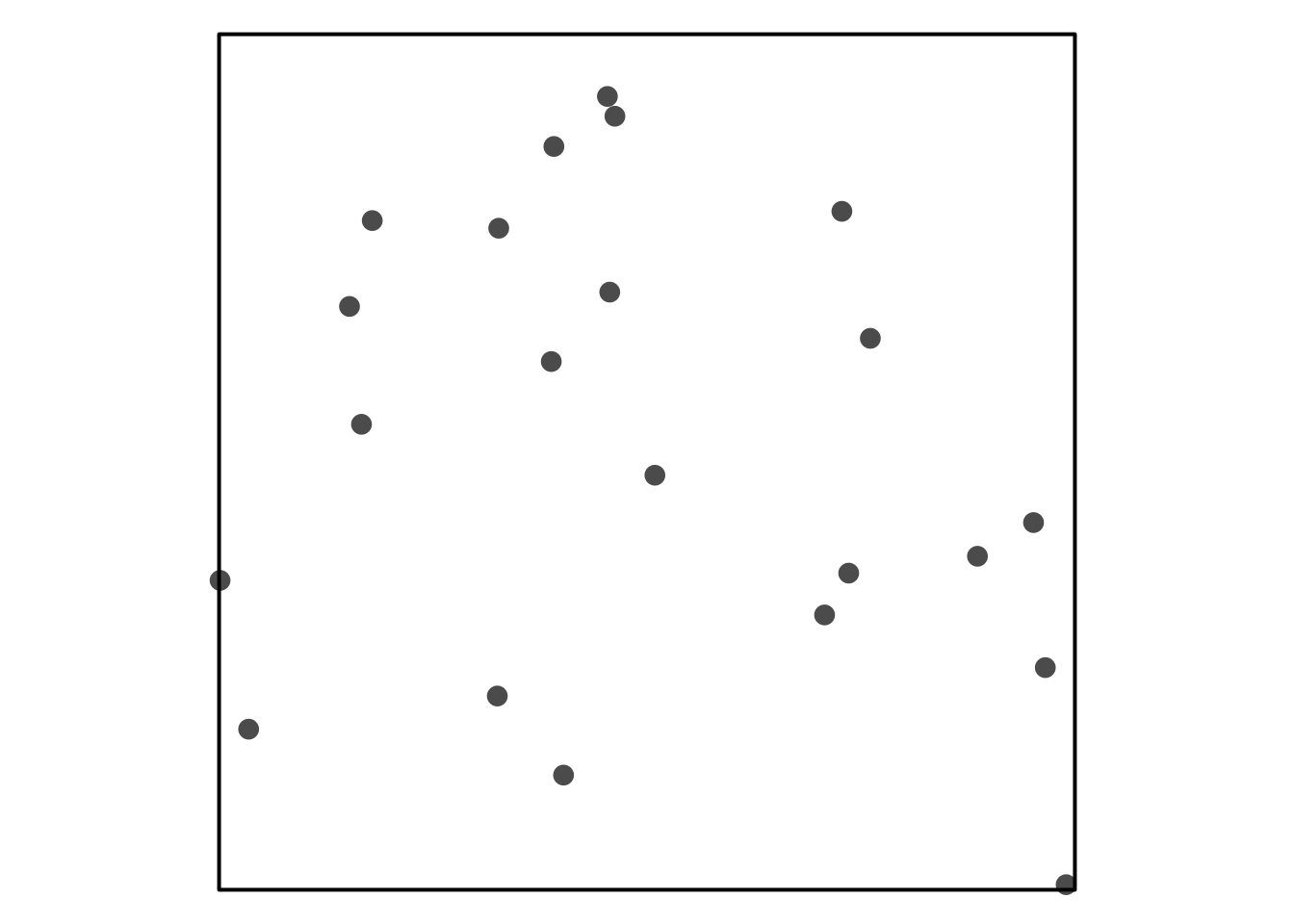
HPP as a null model

  • Interesting theoretical properties, see some soon.
  • Too simple to be a useful model, but a good starting point.
  • Use as a null model - analogous to regression.
  • Identify shortcomings as a starting point for further exploration.

Definitions of a Poisson Process

Recap: many interpretations of the same process

\[ \mathcal{X} = \{(X_1,X_2)^T\}, \quad X \sim \text{MVN} \left(\mathbf{\mu}, \Sigma \right). \]

Or

\[ \mathcal{X} = \{(X_1,X_2)^T\},\]

where

\[ X_1 \sim \mathcal{N}(\mu, \sigma^2), \\ X_2|X_1=x_1 \sim \mathcal{N}\left(\mu_2 + \frac{\sigma_2\rho(x_1 - \mu_1)}{\sigma_1}\ , \ (1 - \rho^2)\sigma_2^2 \right).\]

Recap: many interpretations of the same process

Suggested Poster Topic
  • Can you show the pair-wise equivalence of the definitions I will introduce?
  • Are there any other interpretations that I have missed?

HPP as limit of Binomial Process

Working in continuous time or space is hard. Start discrete and consider the limit

\[\begin{equation*} \{X_1, \ldots, X_m\} \overset{\perp}{\sim} \text{Bern}(p_i). \end{equation*}\]

For now we will let \(p_1 = p_2 = \ldots = p\),

The total number of events in the process:

\[\begin{equation*} N = \sum_{i=1}^{m} X_i \sim \text{Binom}(m , p). \end{equation*}\]

So

\[\begin{equation*} \mathbb{E}[N] = m p, \quad \text{Var}(N) = m p (1-p) \end{equation*}\]

and for \(A \subseteq S\), \(N(A) \sim \text{Binom}\left(\frac{|A|}{|S|}m, p\right).\)

Code 
# histogram ----------

hist_df <- tibble(
n = seq(0, 25),
pdf = dbinom(n, size = 25, prob = 0.3)
)

p_hist <- ggplot(data = hist_df, mapping = aes(x = n, y = pdf)) + 
  geom_col() +
  ylab("Pr(N = n)") +
  zvplot::theme_zv()
 
# grid ----------------
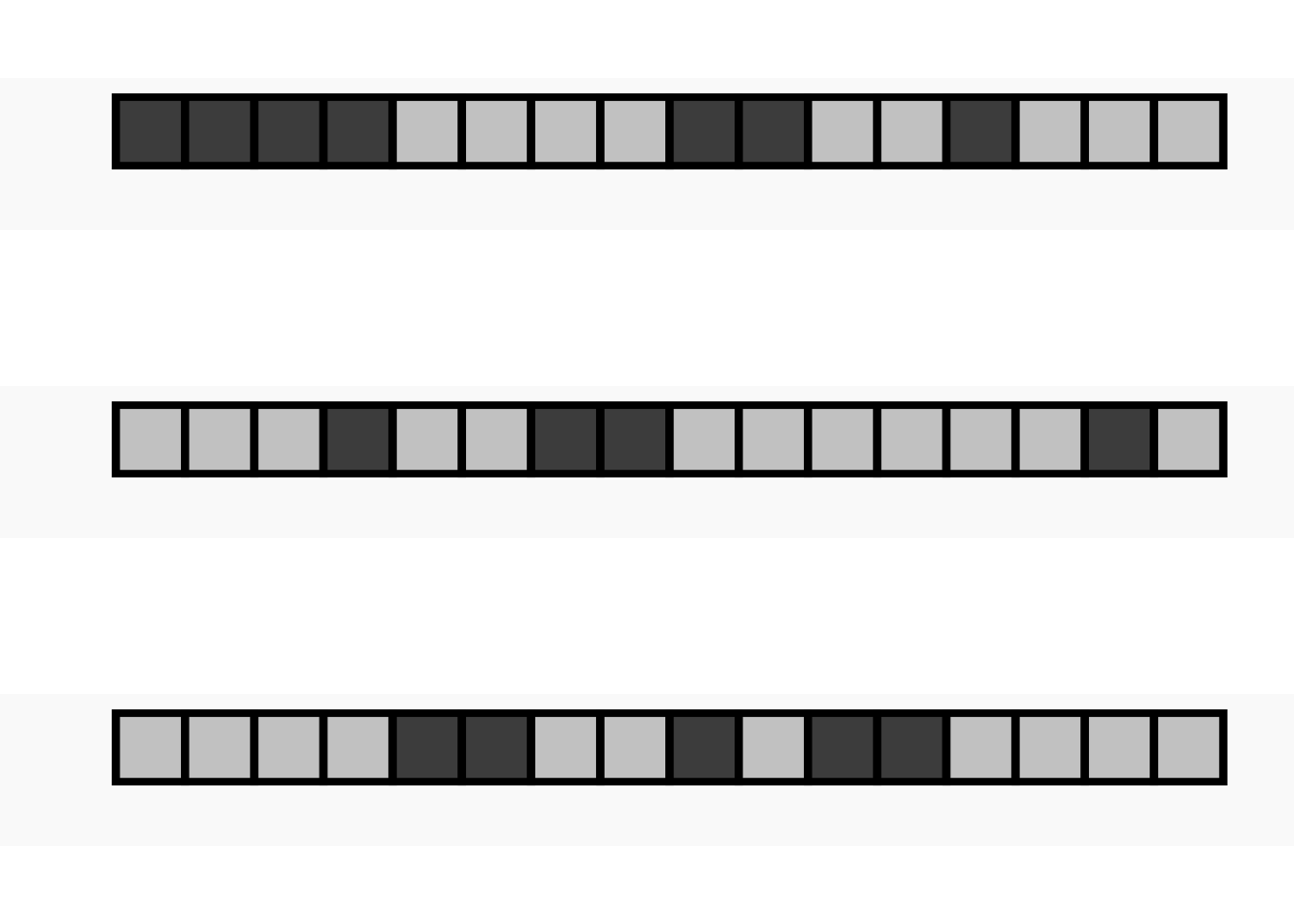
n <- 5 
p <- 0.3

grid_df <- tibble(
  x = rep(1:n, times = n), 
  y = rep(1:n, each = n), 
  z = rbinom(n = n * n, size = 1, prob = p),
  fill_col = if_else(as.logical(z), "grey30", "grey80")
)

p_grid_5 <- ggplot(data = grid_df, aes(x = x, y = y)) + 
  geom_tile(aes(fill = fill_col), col = "black", lwd = 1.5) +
  scale_fill_identity() +
  coord_fixed() + 
  ylab("") +
  xlab("") +
  zvplot::theme_zv()

print(p_hist)
print(p_grid_5)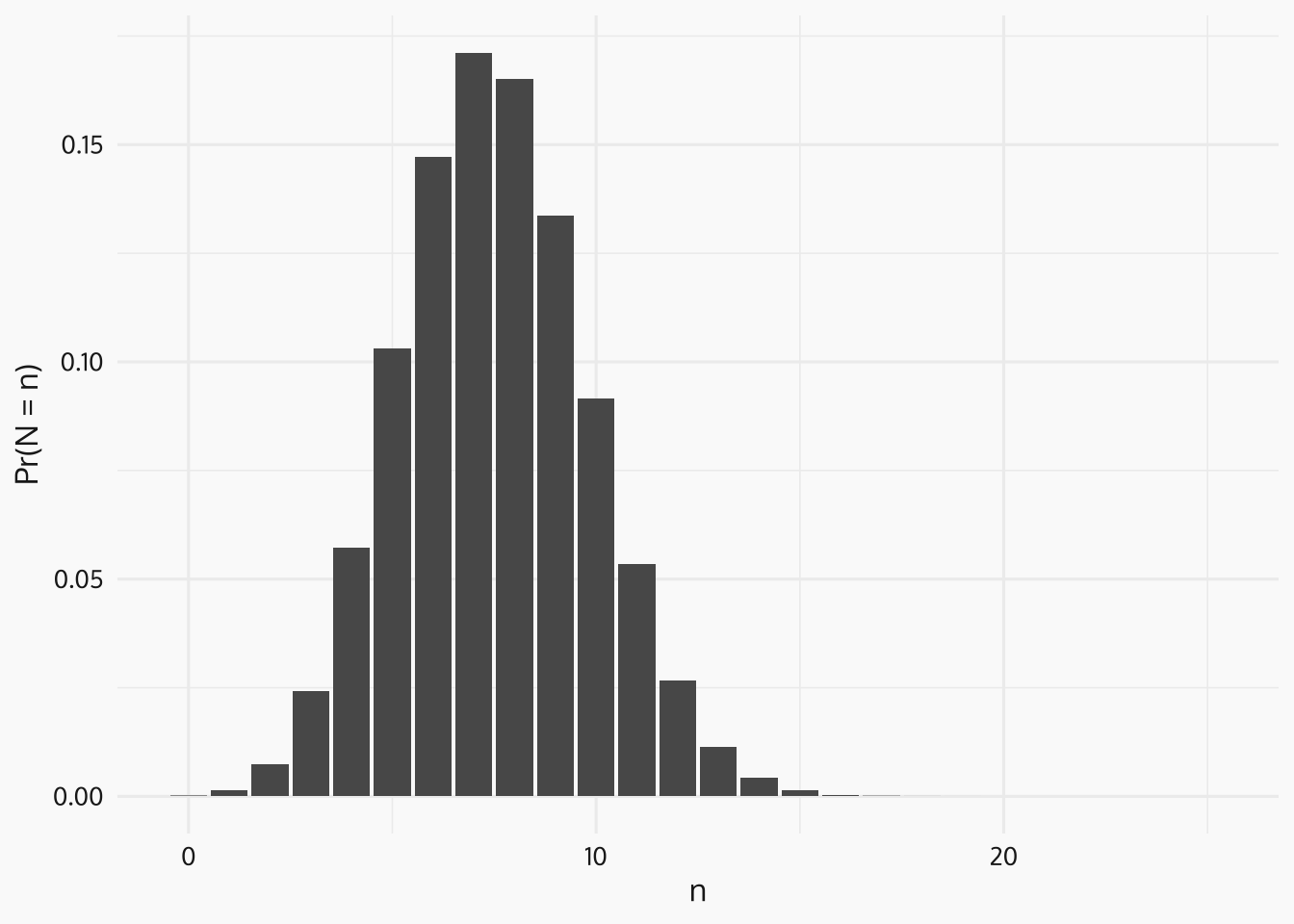

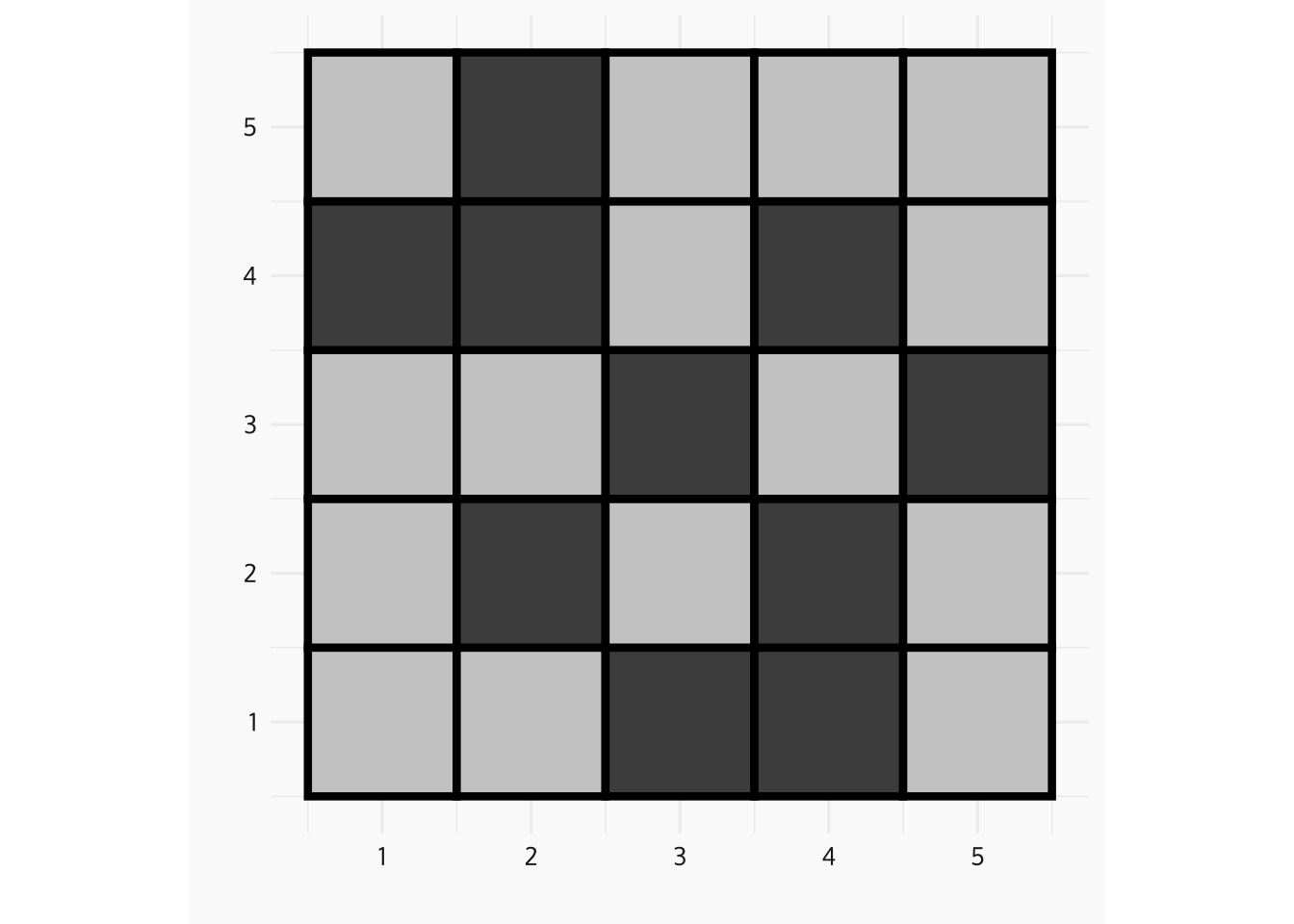
HPP as limit of Binomial Process - Increase the Resolution

Code 
n <- 10 
p <- 0.3 * (5/n)^2

grid_df <- tibble(
  x = rep(1:n, times = n), 
  y = rep(1:n, each = n), 
  z = rbinom(n = n * n, size = 1, prob = p),
  fill_col = if_else(as.logical(z), "grey30", "grey80")
)

p_grid_10 <- ggplot(data = grid_df, aes(x = x, y = y)) + 
  geom_tile(aes(fill = fill_col), col = "black", lwd = 1.5) +
  scale_fill_identity() +
  coord_fixed() + 
  ylab("") +
  xlab("") +
  zvplot::theme_zv() +
  theme(axis.text = element_blank())

print(p_grid_10)

Code 
n <- 20 
p <- 0.3 * (5/n)^2

grid_df <- tibble(
  x = rep(1:n, times = n), 
  y = rep(1:n, each = n), 
  z = rbinom(n = n * n, size = 1, prob = p),
  fill_col = if_else(as.logical(z), "grey30", "grey80")
)

p_grid_20 <- ggplot(data = grid_df, aes(x = x, y = y)) + 
  geom_tile(aes(fill = fill_col), col = "black", lwd = 1) +
  scale_fill_identity() +
  coord_fixed() + 
  ylab("") +
  xlab("") +
  zvplot::theme_zv() +
  theme(axis.text = element_blank())

print(p_grid_20)

Code 
n <- 100 
p <- 0.3 * (5 / n)^2 

grid_df <- tibble(
  x = rep(1:n, times = n), 
  y = rep(1:n, each = n), 
  z = rbinom(n = n * n, size = 1, prob = p),
  fill_col = if_else(as.logical(z), "grey30", "grey80")
)

p_grid_100 <- ggplot(data = grid_df, aes(x = x, y = y)) + 
  geom_tile(aes(fill = fill_col)) +
  scale_fill_identity() +
  coord_fixed() + 
  ylab("") +
  xlab("") +
  zvplot::theme_zv() +
  theme(axis.text = element_blank())

print(p_grid_100)

Looking at the limit: counting specification

  • Each time we increase the resolution by a factor of \(k\) we get more events (in expectation). To keep this constant, we divide \(p\) by an appropriate multiplier.

  • Formally, let \(m \rightarrow \infty\) and \(p \rightarrow 0\) such that \(m p \rightarrow \lambda \in \mathbb{R}^+\). Then

\[\begin{equation*} N(A) \overset{D}{\rightarrow} \text{Pois}(\lambda) \quad \text{ and } \quad N(A) \perp N(B) \text{ when } A \cap B = \emptyset. \end{equation*}\]

This is the counting specification of an HPP.

Inhomogeneous PP and the intensity specification

Generalise by no longer assuming that \(p_1 = \ldots = p_m = p\).

\(N(A) = \sum_{i \in A} X_i\) so \(\Pr(N(A) = n) = \Pr(\sum_{\{i \ :\ a_i \in A\}} X_i = n)\) and:

\[\begin{equation*} \mathbb{E}[N(A)] = \sum_{i=1}^{m} p_i \ \mathbb{I}(a_i \in A), \end{equation*}\]

\[\begin{equation*} \text{Var}(N(A)) = \sum_{i=1}^{m} p_i (1 - p_i) \ \mathbb{I}(a_i \in A). \end{equation*}\]

Introducing the intensity function

Describe the local rate of events by the intensity function:

\[\begin{equation*} \lambda(s) = \lim\left(\frac{ N(s, s+\delta)}{\delta}\right) \quad \text{or} \quad \lambda(\mathbf{s}) = \lim \left( \frac{N(B(\mathbf{s}, \delta))}{|B(\mathbf{s}, \delta)|} \right). \end{equation*}\]

This is known as the intensity specification and for a homogeneous process \(\lambda(s) = \lambda.\)

Counting specification for an IHPP

By considering a similar limit to earlier, you can show that

\[\begin{equation*} N(A) \sim \text{Pois}\left( \int_A \lambda(s) \mathrm{d}s\right) \end{equation*}\]

and \(N(A) \perp N(B)\) when \(A \cap B = \emptyset\), where


\(\Lambda(A) = \int_A \lambda(s) \mathrm{d}s\) is known as the integrated intensity function or the compensator.

Suggested Activity

Can you prove this result?

Example IHPP

For an IHPP, events are located independently over \(S\) in proportion to \(\lambda(s)\).

grid_df <- as_tibble(expand.grid(x = seq(-3, 3, length.out = 401), y = seq(-3, 3, length.out = 401)))

grid_df$r <- sqrt(grid_df$x^2 + grid_df$y^2)

grid_df$lambda <- grid_df$r

n_sampled <- rpois(n = 1, sum(grid_df$lambda * (6/401)^2))
sampled_squares <- sample(1:401^2, size = n_sampled,prob = grid_df$lambda, replace = TRUE)
sampled_locations <- tibble(.rows = n_sampled)
sampled_locations$x <- grid_df$x[sampled_squares] + runif(n_sampled, -3/401, 3/401)
sampled_locations$y <- grid_df$y[sampled_squares] + runif(n_sampled, -3/401, 3/401)

ggplot(data = grid_df) +
  geom_tile(mapping = aes(x = x, y = y, fill = lambda)) + 
  coord_fixed() +
  geom_point(data = sampled_locations, aes(x = x, y = y), col = "white") +
  zvplot::theme_zv()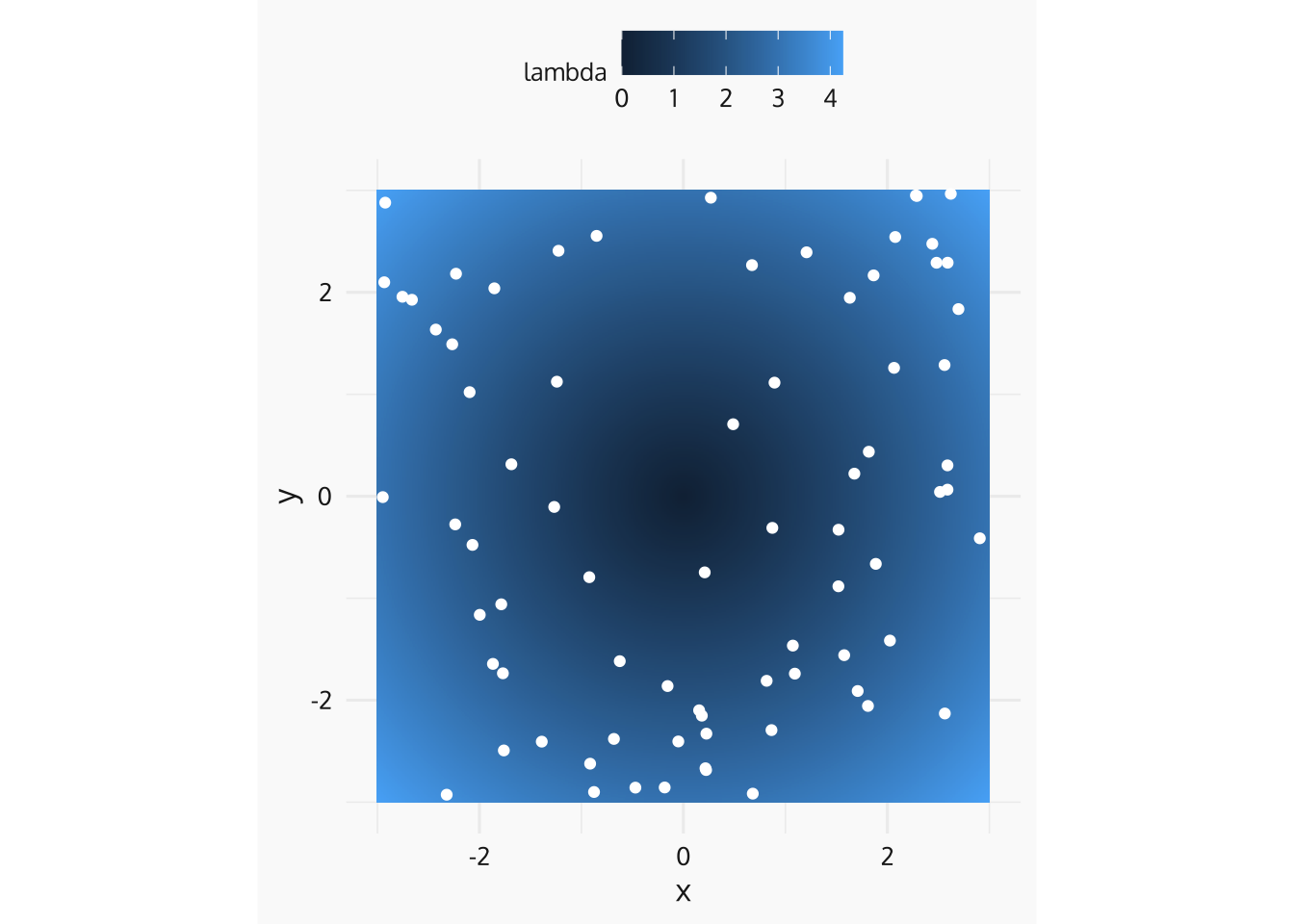

Special cases in 1 dimension

The Interval Specification

Define \(T_1 = X_i\) and \(T_i = X_i - X_{i-1}\) for \(i \geq 2\).

A homogeneous Poisson process has

\[\begin{equation*} T_i \overset{i.i.d.}{\sim} \text{Exp}(\lambda). \end{equation*}\]

An inhomogeneous Poisson process, the \(i^{\text{th}}\) inter-arrival time has pdf:

\[\begin{equation*} f_{T_i}( t \ | \ x_i) = \lambda(x_i + t)\exp \left\{ - \int_{x_i}^{x_i +t}\lambda(t)\mathrm{d}t\right\} \quad \text{ for } t \geq 0. \end{equation*}\]

Suggested Poster Topic

Can you prove these results yourself, using a similar limiting argument about the Geometric distribution?

The Counting Process Specification

Consider the cumulative number of points as a continuous time stochastic process.

  • Highly dependent
  • Exponential step lengths
  • Almost surely unit step heights
n <- 20
T_i <- rexp(n)
X_i <- cumsum(T_i)
N_i <- seq(1, n)
t_min <- 0 
t_max <- 1.1 * max(X_i)

x <- c(t_min, rep(X_i, each = 2), t_max)
y <- c(0, 0, rep(N_i, each = 2))
plot(
  x = x,
  y = y,
  xlim = c(t_min, t_max), 
  ylim = c(0, 1.4 * n),
  type = "l", 
  lwd = 1.5, 
  bty = "n",
  xlab = "t", 
  ylab = expression(N[t]))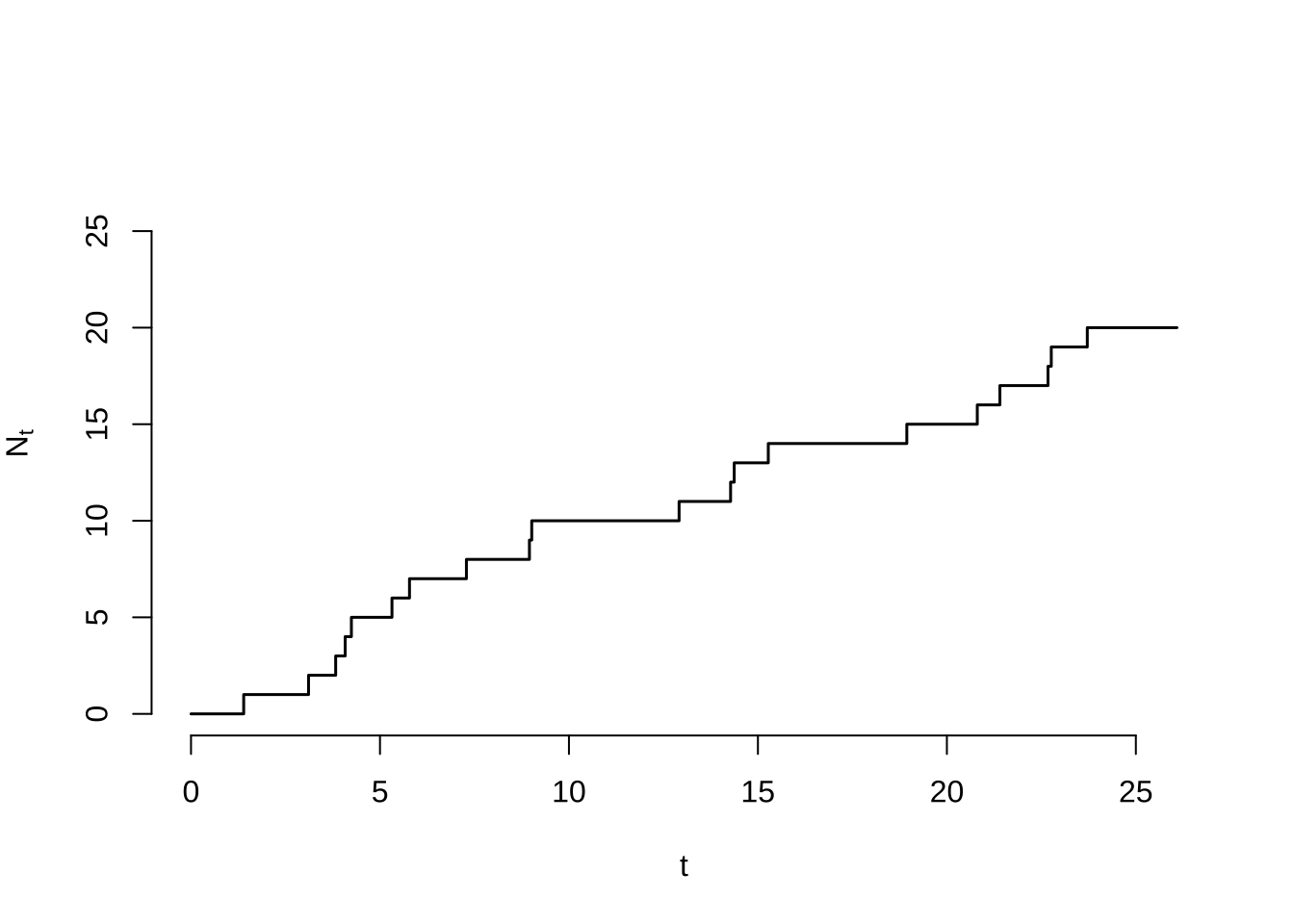

Other Useful Properties

Superposition is like point process addition.

Random Thinning is like point process division.

Poisson processes are closed under superposition and random thinning. Can you prove this?

Areas for Further Exploration

  • Testing for CSR using these properties?

    • difficulties with finite regions (edge effect corrections)
    • complications for \(\lambda(t)\) non-constant (Ripley’s \(K\)-function)

  • How could these properties be used to simulate point patterns?

  • What happens if you relax some of these assumptions? E.g. Gamma inter-arrivals, points generated near existing points…

References

Numata, Makoto. 1961. “Forest Vegetation in the Vicinity of Choshi. Coastal Flora and Vegetation at Choshi, Chiba Prefecture IV.” Bulletin of Choshi Marine Laboratory, Chiba University 3: 28–48.
Ripley, Brian D. 1977. “Modelling Spatial Patterns (with Discussion).” Journal of the Royal Statistical Society: Series B (Methodological) 39 (2): 172–212.
Strauss, David J. 1975. “A Model for Clustering.” Biometrika 62 (2): 467–75.